Notice
Recent Posts
Recent Comments
Link
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
Tags
- Vivado
- 자격증
- 리눅스
- java
- Backjoon
- axi
- 정보처리기사
- amba
- linux
- Beakjoon
- 정처기
- HDLBits
- AMBA BUS
- 코딩테스트
- UNIX
- baekjoon
- boj
- C++
- Zynq
- verilog
- 실기
- hdl
- 백준
- chip2chip
- verilog HDL
- Xilinx
- FPGA
- vitis
- Bus
- SQL
Archives
- Today
- Total
Hueestory
[1707] 이분 그래프 (C++) 본문
#include <iostream>
#include <vector>
#include <queue>
#include <algorithm>
#define X 1
#define Y 2
using namespace std;
int v, e;
vector<vector<int>> A;
vector<int> visited;
void DFS(int start, int color);
bool isBipartite();
int main() {
ios::sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);
int k; cin >> k;
// k 만큼 반복
for (int i = 0; i < k; i++) {
cin >> v >> e;
A.resize(v + 1);
visited.resize(v + 1, 0);
// 에지의 개수 만큼 반복
for (int j = 0; j < e; j++) {
int a, b; cin >> a >> b;
// 인접 리스트 구현
A[a].push_back(b);
A[b].push_back(a);
}
// 그래프의 모든 노드를 탐색하기 위함
for (int z = 1; z <= v; z++) {
if (!visited[z]) DFS(z, X); // 방문하지 않았다면 초기 색을 X로 설정 후 DFS 탐색
}
if (isBipartite()) cout << "YES\n";
else cout << "NO\n";
A.clear();
visited.clear();
}
return 0;
}
void DFS(int start, int color) {
visited[start] = color;
// 각 노드에서 연결된 노드의 개수만큼 반복
for (int i = 0; i < A[start].size(); i++) {
int next = A[start][i];
if (!visited[next]) { // 방문하지 않았다면
DFS(next, color == X ? Y : X); // next를 start로 지정, 삼항 연산자를 사용해 색 지정
}
}
}
bool isBipartite() {
// 노드의 개수 만큼 반복
for (int i = 1; i <= v; i++) {
for (int j = 0; j < A[i].size(); j++) {
int next = A[i][j];
if (visited[i] == visited[next]) return false; // 현재 노드와 다음 노드의 색이 같을 경우 이분 그래프가 아님
}
}
return true;
}
DFS를 이용한 이분 그래프 판별 문제
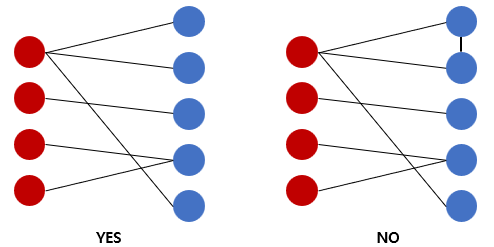
1. 값을 입력 받아 연결 리스트 형태로 그래프를 저장
2. 색 X, Y를 선언하고 각 노드의 색을 설정하는 방식 사용
3. DFS를 통해 모든 노드를 탐색하고 색을 지정한다
4. isBipartite 함수에서 현재 노드와 다음 노드의 색이 같은지 판별하고, 같을 경우 이분 그래프가 아니다

'PS > BOJ' 카테고리의 다른 글
| [2251] 물통 (C++) (1) | 2024.06.03 |
|---|---|
| [1325] 효율적인 해킹 (C++) (0) | 2024.05.28 |
| [18352] 특정 거리의 도시 찾기 (C++) (0) | 2024.05.28 |
| [1033] 칵테일 (C++) (0) | 2024.05.23 |
| [1850] 최대공약수 (C++) (0) | 2024.05.23 |
Comments




